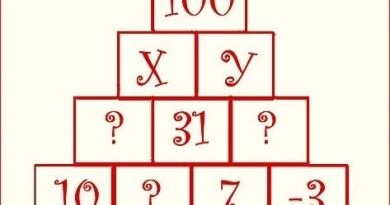
A man wanted to get into his work building, but he had forgotten his code. However, he did remember five clues. These are what those clues were:
The fifth number plus the third number equals fourteen.
The fourth number is one more than the second number.
The first number is one less than twice the second number.
The second number plus the third number equals ten.
The sum of all five numbers is 30.
What were the five numbers and in what order?

7, 4, 6, 5, 8