#1521 - Math Algebra Problem
You are given with the following sum. Each of the letters can be decoded as a digit. If we tell you that D = 5, then can you solve it entirely?
DONALD
+GERALD
=ROBERT

526485
+197485
=723970
You are given with the following sum. Each of the letters can be decoded as a digit. If we tell you that D = 5, then can you solve it entirely?
DONALD
+GERALD
=ROBERT

526485
+197485
=723970
Three fair coins are tossed in the air and they land with heads up. Can you calculate the chances that when they are tossed again, two coins will again land with heads up?

50%
The vents in this case are independent. If you form the possible outcomes, they will be as follows
HHH
HTT
HHT
HTH
TTT
TTH
THT
THH
Now among these outcomes, four will give the required results. Thus the probability is 50%.
Given that
(78)^9 = 6
And (69)^4 = 11
Can you find out (89)^2 = ?
7 + 8 = 15 and 15 - 9 = 6
6 + 9 = 15 and 15 - 4 = 11
Thus, (89)^2:
8 + 9 = 17 and 17 - 2 = 15
Can you count the number of triangles in the given picture?
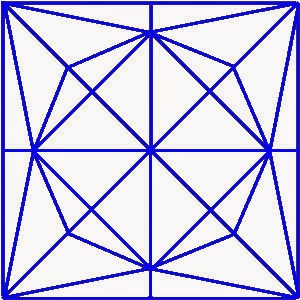
There are 92 triangles in this picture.
A rain drop fell from one leaf to another leaf and lost 1/4th of its volume. It then fell to another leaf and lost 1/5th of the volume. It again fell on another leaf and lost 1/5th of the volume.
This process kept repeating till it fell on the last leaf losing 1/75th of its volume.
Can you calculate the total percentage of loss from the initial volume when the drop has fallen to the last leaf accurate up to two decimal places?

4%
Let us assume that the initial volume of the water drop was k.
k - (1/4) k = (3/4) k
(3/4) k - (1/5) [(3/4) k] = (3/4) k * [1 - (1/5)] = (3/4) k * (4/5) = (3/5) k
(3/75) k = (1/25) k
1/25 = 4%
Thus, the answer is four percent.
Bobby and Wilbur decided to take their respective car out of the garage and race. None of them cheated and they both stood at the start time and decided to cover a distance in full throttle. The first to reach the mark was to be declared the winner.
Upon reaching the finishing mark, they found out that Bobby car is 1.2 times faster than Wilbur. Now, Wilbur had reached the mark about 1 minute and 30 seconds later than Bobby. Bobby car reached the mark at 60 MPH on average.
Can you calculate the distance between the starting mark and the final mark with the help of the given data?

7.5 Miles
(Speed of Bobby) = 60 MPH = 1.2 x (Speed of Wilbur) [MPH] = 1 M/ min
Thus (Speed of Wilbur) = 60/1.2 [MPH] = 50 [MPH] = 5/6 M/ min
(Time of Wilbur) = D [M] / (Speed of Wilbur) [M/min] = D/ (Speed of Wilbur) [min] = D/(5/6) min = 6D/5 min = 1.2 D min
(Time of Bobby) = D [M] / (Speed of Bobby) [M/min] = D/ (Speed of Bobby) [min] = D/(1) min = D min
Since (Time of Wilbur) - (Time of Bobby) = 1.5 min
Then (1.2 - 1) D min = 0.2D min = 1.5 min
Therefore D = 1.5/0.2 M = 1.5*5 = 7.5 Miles
Can you find any error in the following sentence?
A taxi was standing outside a fort at night. A man came out of the fort, opened the gate and hit the taxi driver killing him instantly. He took out all the money out of the meter and started running till he was caught by a local sheriff.

There is no money in the taxi meter. It just consist of a timer. The children from small towns might not be aware of the fact.
Suppose that you are trapped on the surface of a frozen lake. The surface is so smooth and ideal that there is no friction at all. You cant make any grip on the ice and no wind is blowing to help you out. You have just a mobile phone with you which has got no reception disabling you to call for help.
How will you plan your escape before you freeze to death on the frozen lake?
You have been told that the floor is ideally frictionless. Thus, all you need to do is throw your mobile phone in the opposite direction and the throw will propel you in the other direction. Since there is no friction, you will be able to glide smoothly to one side even with as little kick as this. This is same as firing a gun.
Can you find out the total number of triangles in the given figure?
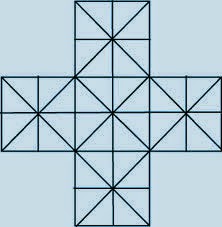
There are 60 triangles in the given figure.