#2321 - Solve Rebus Puzzle
can you solve the below rebus puzzle
Reduction
#2322 - Infosys Written Aptitude Interview Quest
Alex speaks truth only once a day in a week. Below are a few hints for you:
First: Days are Sunday, Monday and so on.
Second: One day he says, "I lie on Monday and Tuesday".
Third: On the next day, he says, "Today is either Thursday, Saturday or Sunday".
Fourth: On the next day, he says, "I lie on Wednesday and Friday".
Can you identify the day on which he speaks truth?
Alex speaks truth on Thursday.
#2323 - Easy Algebra Problem
If,
9 * 8 * 7 = 65
8 * 7 * 6 = 50
7 * 6 * 5 = 37
Find
6 * 5 * 4 = ?
26, (5 * 4) + 6 = 26
#2324 - This Old One Runs Forever Riddle
A couple went to a hill station for enjoying their vacation.They have 12 sons and each son have a wife who have 3 sons further.
How many people went to the hill station?
2
Read the question again. The questions say that a couple went to hill station. There is no mention that the further mentioned people also went along.Thus the answer is two people
#2326 - Solve Algebraic Equation
ONE
ONE
ONE
THREE
THREE
ELEVEN
---------
TWENTY
If O, T and E are not zero, and all the letters have a distinct value, can you solve for the letters?
O=2, N=3, E=5, T=6, H=9, R=7, L=0, V=1, W=4, Y=8
Only then,
One + One + One + Three + Three + Eleven = Twenty
235 + 235 + 235 + 69755 + 69755 + 505153 = 645368
#2327 - Tic Tac Toe Riddle
This is basically a game of Tic-Tac-Toe which you all might have played innumerable times. Here, we are playing with the black and white markers instead. Also, there is a bit change to the rules. The changed rules allows you to play just three times. After the three markers are put by each of the players, you can only slide your marker into an empty square that shares a common wall with the square that the marker is leaving.You can refer to the figure given. If this is the position of the game, the white's next move would be from 6 to 3. Now, whatever the black does, the white one will move his marker from 5 to 2 and he will have a three in a row.What you have to decide is if both of the players are using a perfect strategy, will the white player (who plays first) always win? Or it will be the black one who will win always? Or every game will be a draw?
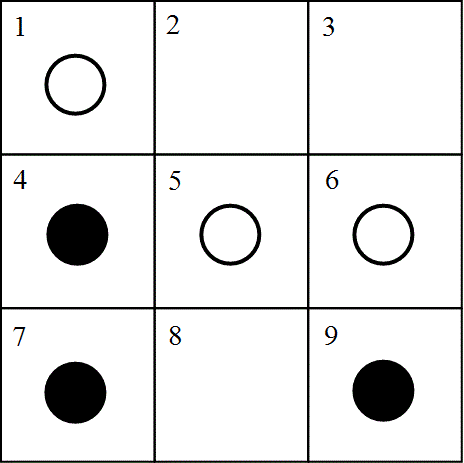
Let us try and make the white win when black's first move is to a non-corner square. White begins at 5 and black places its first marker at 2. White puts at 9 and black puts at 1. White plays at 3. Now if black puts at 7 to block, white will move from 5 to 6 and will win. But in this game, black can only play his last marker at 6. White can't win on the next move as his market at square 9 won't be able to get to square 7 in a single move. But white cam get to square 7 before black can block him or win. White will move from 8 to 7 to win the game. Thus, white can always force a win if he starts from the center of the square.
#2329 - Maths Sets Problem
Jim has three close friends at his school: Michael, John and Alice. Two of them play football, two play basketball and two play hockey. The friend who does not play hockey does not play basketball as well. The friend who does not play football, does not play hockey.
Can you identify which sport/s is played by which person?
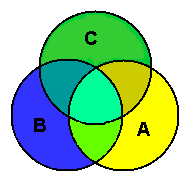
John and Michael play all the three sports. Alice plays none.
This is after assuming that girls do not play football. If in case, the school had a girl's football league, we would know only that one of the three play no sports at all and the others play all three.
#2330 - Chinese Checkers Puzzle
See the given image carefully. What you have to do is move the blue checkers in the position of the black checkers and vice versa. You are only allowed to move the checker to an adjacent empty space. Do it in the least possible moves.
1 -> 4
6 -> 1
2 -> 6
5 -> 2
4 -> 5
Of course, you can do in a different manner, this is just one of the possible solution with least number of moves.