#1 - Smart Math Problem

As they say, beggars can't be choosers, in fact begger take what they can get. A begger on the street can make one cigarette out of every 6 cigarette butts he finds. After one whole day of searching and checking public ashtrays the begger finds a total of 72 cigarette butts. How many cigarettes can he make and smoke from the butts he found?

Smart Math Problem
View Answer Discuss

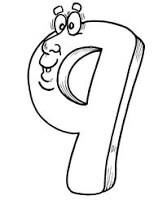
14
If the begger can make a whole cigarette from 6 butts then he can make 12 cigarettes from the 72 he found. Once he smokes those, he then will have another 12 butts, which gives him enough to make another 2 cigarettes. A total of 14.

#2 - Maths Handshake Puzzle

At a party, everyone shook hands with everybody else. There were 66 handshakes. How many people were at the party?

Maths Handshake Puzzle
View Answer Discuss

12

In general, with n+1 people, the number of handshakes is the sum of the first n consecutive numbers: 1+2+3+ ... + n.
Since this sum is n(n+1)/2, we need to solve the equation n(n+1)/2 = 66.
This is the quadratic equation n2+ n -132 = 0. Solving for n, we obtain 11 as the answer and deduce that there were 12 people at the party.

Since 66 is a relatively small number, you can also solve this problem with a hand calculator. Add 1 + 2 = + 3 = +... etc. until the total is 66. The last number that you entered (11) is n.

#3 - Hardest Mathematical Columbus Puzzle

The Puzzle: Here is a famous prize problem that Sam Loyd issued in 1882, offering $1000 as a prize for the best answer showing how to arrange the seven figures and the eight 'dots' .4.5.6.7.8.9.0. which would add up to 82

View Answer Discuss

The dot over a number signifies that it is a repeater which would go on for ever, as when we endeavor to describe 1/3 decimally as 0.33333 . . . . (etc)
With a series of numbers we place the dot over the first and last, as with 0.97979797979 . . . (etc)
The remarkable feature being that a proper fraction divided by 9s e.g. 46/99 is exactly equal to the numerator with the repeater sign followed by the decimal.

#4 - Maths Equation Puzzle

I know a way by which i can make i can get total of 120 by using five zeros 0,0,0,0,0 and any one mathematical operator.
Do you ?

Maths Equation Puzzle
View Answer Discuss

(0!+0!+0!+0!+0!)!
=(1+1+1+1+1)!
=(4)!
=5! is 5*4*3*2*1=120

#5 - Answer a Maths Riddle

Can you find a seven digit number which describes itself. The first digit is the number of zeros in the number. The second digit is the number of ones in the number, etc. For example, in the number 21200, there are 2 zeros, 1 one, 2 twos, 0 threes and 0 fours.

View Answer Discuss

3211000

#6 - Brain Twister Puzzle

2+3=8,
3+7=27,
4+5=32,
5+8=60,
6+7=72,
7+8=??

Solve it?

View Answer Discuss

98

2+3=2*[3+(2-1)]=8
3+7=3*[7+(3-1)]=27
4+5=4*[5+(4-1)]=32
5+8=5*[8+(5-1)]=60
6+7=6*[7+(6-1)]=72
therefore
7+8=7*[8+(7-1)]=98
x+y=x[y+(x-1)]=x^2+xy-x

#7 - Tough Age Puzzle

My grandson is about as many days as my son in weeks, and my grandson is as many months as I am in years. My grandson, my son and I together are 120 years. Can you tell me my age in years ?

Tough Age Puzzle
View Answer Discuss

I am 72 years old.

Let m be my age in years. If s is my son's age in years, then my son is 52s weeks old. If g is my grandson's age in years, then my grandson is 365g days old. Thus,
365g = 52s.
Since my grandson is 12g months old,
12g = m.
Since my grandson, my son and I together are 120 years,
g + s + m = 120.
The above system of 3 equations in 3 unknowns (g, s and m) can be solved as follows.
m / 12 + 365 m / (52 x 12) + m = 120 or
52 m + 365 m + 624 m = 624 x 120 or
m = 624 x 120 / 1041 = 72.
So, I am 72 years old.

#8 - Tricky Equation Puzzle

Can you arrange four 9's and use of atmost 2 math symbols , make the total be 100?

Tricky Equation Puzzle
View Answer Discuss

99 / .99

#9 - Weighing Balance Puzzle

You can place weights on both side of weighing balance and you need to measure all weights between 1 and 1000. For example if you have weights 1 and 3,now you can measure 1,3 and 4 like earlier case, and also you can measure 2,by placing 3 on one side and 1 on the side which contain the substance to be weighed. So question again is how many minimum weights and of what denominations you need to measure all weights from 1kg to 1000kg.

Weighing Balance Puzzle
View Answer Discuss

For this answer is 3^0, 3^1, 3^2... That is 1,3,9,27,81,243 and 729.

#10 - February Maths Puzzle

Using eight eights and addition only, can you make 1000?

February Maths Puzzle
View Answer Discuss

888 + 88 + 8 + 8 + 8 = 1000